Continuous Probability Distributions, Normal Distribution - IB Maths HLHow can we find the standard deviation of the weight of a population of cats which is found to be normally distributed with mean 2.1 Kg and the 60% of the dogs weigh at least 1.9 Kg.
IB Mathematics HL – Continuous Probability Distribution, Normal Distribution
A normal distribution is a continuous probability distribution for a random variable X. The graph of a normal distribution is called the normal curve. A normal distribution has the following properties.
1. The mean, median, and mode are equal.
2. The normal curve is bell shaped and is symmetric about the mean.
3. The total are under the normal curve is equal to one.
4. The normal curve approaches, but never touches, the x-axis as it extends farther and farther away from the mean.
Approximately 68% of the area under the normal curve is between

and
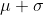
and . Approximately 95% of the area under the normal curve is between

and
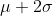
. Approximately 99.7% of the area under the normal curve is between
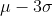
and
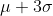
The standard normal distribution is a normal probability distribution that has a mean of 0 and a standard deviation of 1.
)
Concerning your question
Let the random variable
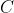
denotes the weight of the cats, so that
)
We know that
=0.6)
Since we don’t know the standard deviation, we cannot use the inverse normal. Therefore we have to transform the random variable
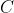
to that of
)
, using the transformation
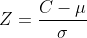
we have the following
=0.6%20\Rightarrow%20P(\frac{C-%202.1}{\sigma}%20\geq%20\frac{1.9-%202.1}{\sigma})=0.6)
=0.6)
Using GDC Casio fx-9860G SD
MAIN MENU > STAT>DIST(F5)>NORM(F1)>InvN>
Setting Tail: right
Area: 0.6
:1
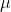
:0
We find that the standardized value is -0.2533471
Therefore,
)
