Big overall changes are that matrices have been removed. The two portfolio
pieces have been replaced by a more open-ended mathematical exploration. Applications are mentioned
much more than previously.
Algebra
Arithmetic sequences and series, sum of finite arithmetic series, geometric sequences and series, sum of finite and infinite geometric series,Sigma notation.
Exponents and logarithms,Laws of exponents, laws of logarithms,Change of base.
Counting principles, including permutations and combinations.
The binomial theorem
Proof by mathematical induction.
Complex numbers: the number i
terms real part, imaginary part, conjugate,modulus and argument.
Cartesian form z = a + ib
Sums, products and quotients of complex numbers
Modulus–argument (polar) form, The complex plane.Powers of complex numbers: de Moivre’s theorem.
nth roots of a complex number
Conjugate roots of polynomial equations with real coefficients.
Solutions of systems of linear equations (a maximum of three equations in three unknowns), including cases where there is a unique solution, an infinity of solutions or no solution.
Functions and equations
Concept of function (domain, range, image),Odd and even functions,Composite functions, Identity function,One-to-one and many-to-one functions
Inverse function, The graph of a function, Investigation of key features of graphs, such as maximum and minimum values, intercepts, horizontal and vertical asymptotes and symmetry,and consideration of domain and range.
Transformations of graphs: translations, stretches, reflections in the axes. The graph of the inverse function as a reflection in y = x. Rational function, exponential function and logarithmic function.
Polynomial functions and their graphs. The factor and remainder theorems. The fundamental theorem of algebra.
Solving quadratic equations using the quadratic formula. Use of the discriminant to determine the nature of the roots.
Solving polynomial equations both graphically and algebraically. Sum and product of the roots of polynomial equations.
Use of technology to solve a variety of equations, including those where there is no appropriate analytic approach.
Graphical or algebraic methods, for simple polynomials up to degree 3. Use of technology for these and other functions.
Circular functions and trigonometry
The circle: radian measure of angles. Length of an arc; area of a sector.Definition of cosθ , sinθ and tanθ in terms of the unit circle.
Exact values of sin, cos and tan of
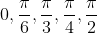
and their multiples.
Definition of the reciprocal trigonometric ratios secθ , cscθ and cotθ . Pythagorean identities.
Compound angle identities. Double angle identities.
Composite functions of the form f (x) = asin(b(x + c)) + d .
The inverse functions arcsin x ,arccos x , arctan x , their domains and ranges, their graphs.
Algebraic and graphical methods of solving trigonometric equations in a finite interval, including the use of trigonometric identities and factorization.
The cosine rule. The sine rule including the ambiguous case. Area of a triangle
Vectors
Concept of a vector. Representation of vectors using directed line segments. Unit vectors; base vectors i, j, k.Components of a vector.
The definition of the scalar product of two vectors.
Properties of the scalar product:
The angle between two vectors. Perpendicular vectors; parallel vectors. vVector equation of a line in two and three dimensions: r = a +λb .
Simple applications to kinematics. The angle between two lines.Coincident, parallel, intersecting and skew lines.
Points of intersection. The definition of the vector product of two vectors.
Properties of the vector product. Geometric interpretation of v × w .
Vector equation of a plane r = a +λb + μc .
Use of normal vector to obtain the form r ⋅ n = a ⋅ n.
Cartesian equation of a plane ax + by + cz = d .
Intersections of: a line with a plane; two planes; three planes. Angle between: a line and a plane; two planes.
Statistics and probability
Concepts of population, sample, random sample and frequency distribution of discrete and continuous data.
Grouped data: mid-interval values, interval width, upper and lower interval boundaries. Mean, variance, standard deviation.
Concepts of trial, outcome, equally likely outcomes, sample space (U) and event.
The probability of an event A. The complementary events A and A′ (not A). Use of Venn diagrams, tree diagrams, counting principles and tables of outcomes to solve problems.
Combined events; the formula for P(A∪ B) . Mutually exclusive events. Conditional probability. Independent events, the definition. Use of Bayes’ theorem for a maximum of three events.
Concept of discrete and continuous random variables and their probability distributions. Definition and use of probability density functions.
Expected value (mean), mode, median, variance and standard deviation.
Binomial distribution, its mean and variance. Poisson distribution, its mean and variance.
Normal distribution, Properties of the normal distribution. Standardization of normal variables.
Calculus
Informal ideas of limit, continuity and convergence. Definition of derivative from first principles.
The derivative interpreted as a gradient function and as a rate of change. Finding equations of tangents and normals.
Identifying increasing and decreasing functions.
The second derivative. Higher derivatives.
Derivatives of xn , sin x , cos x , tan x ,
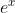
and ln x . Differentiation of sums and multiples of functions.
The product and quotient rules. The chain rule for composite functions.
Related rates of change. Implicit differentiation.
Derivatives of sec x , csc x , cot x ,
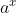
, loga x ,arcsin x , arccos x and arctan x .
Local maximum and minimum values. Optimization problems. Points of inflexion with zero and non-zero gradients.
Graphical behaviour of functions, including the relationship between the graphs of f , f ′ and f ′′ .
Indefinite integration as anti-differentiation. Indefinite integral of x^n , sin x , cos x and
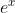
.
Anti-differentiation with a boundary condition to determine the constant of integration. Definite integrals.
Area of the region enclosed by a curve and the x-axis or y-axis in a given interval; areas of regions enclosed by curves.
Volumes of revolution about the x-axis or y-axis.
Kinematic problems involving displacement s, velocity v and acceleration a. Total distance travelled.
Integration by substitution. Integration by parts.